Armonografo a due pendoli oscillazione laterale

I due pendoli dell'armonografo oscillano in modo perpendicolare uno all'altro, ossia uno si muove da nord a sud e l'altro da est a ovest. Se solleviamo al massimo le aste di due pendoli che sono lunghe uguali e le rilasciamo contemporaneamente, otteniamo una linea diagonale, avremo perciò una curva chiusa, mentre se uno dei pendoli viene rilasciato quando l'altro è a metà del suo percorso, otteniamo una circonferenza. ossia un curva aperta.



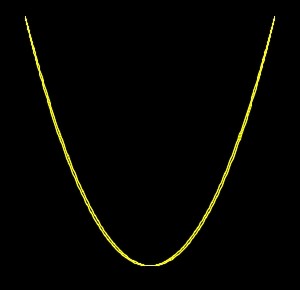
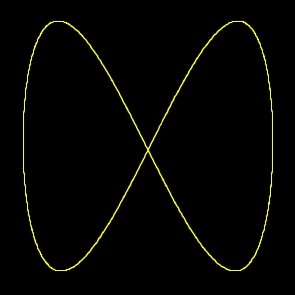
n.1) Unisono. 1:1 chiusa     n.2) Unisono. 1:1 aperta
I due pendoli hanno la stessa lunghezza e vengono rilasciati insieme, curva chiusa. I due pendoli hanno la stessa lunghezza e vengono rilasciati quando uno è a metà percorso dell'altro, curva aperta.

Se spostiamo la posizione del peso appeso ad una delle aste dei due pendoli avremo due diverse velocità nelle oscillazioni, che influenzeranno la forma del disegno.


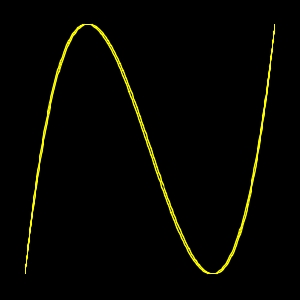
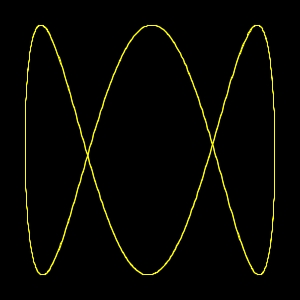
n.3) Ottava. 2:1 chiusa     n.4) Ottava. 2:1 aperta

L'oscillazione di uno dei due pendoli ha una velocità doppia, dell'altro, e vengono rilasciati insieme, curva chiusa. Un pendolo ha ancora una velocità doppia dell'altro ma è rilasciato quando è l'altro già a metà del suo percorso, curva aperta.

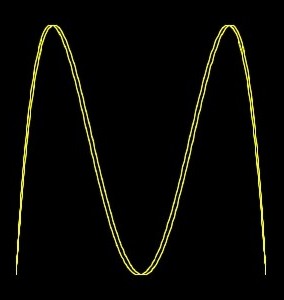
n.5) 3:1 chiusa     n.6) 3: 1 aperta
Un dei due pendoli ha una velocità tripla dell'altro e vengono rilasciati insieme, curva chiusa. Come il precedente, ma viene rilasciato a metà percorso dell'altra, curva aperta.

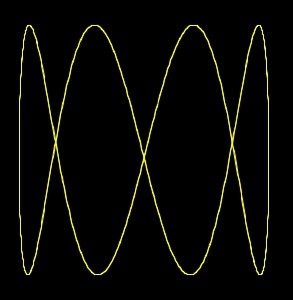
n.7) 4:1 chiusa     n.8) 4: 1 aperta
Un dei due pendoli ha una velocità quadrupla dell'altro e vengono rilasciati insieme, curva chiusa.
Quando l'altro viene rilasciato a metà percorso abbiamo, curva aperta.

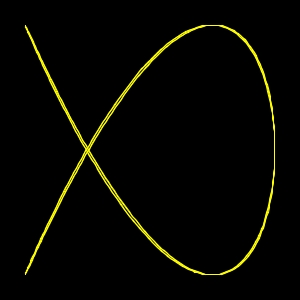
n.9) 3:2 chiusa     n.10) 3: 2 aperta
Nell'intervallo di Quarta, un pendolo compie 3 oscillazioni mentre l'altro ne fa due.
Se partono insieme, curva chiusa, na se uno parte a metà percorso dell'altro, abbiamo la curva aperta.

n.11) 4:3 chiusa     n.12) 4: 3 aperta
Nell'intervallo di Quinta, un pendolo compie 4 oscillazioni mentre l'altro ne fa 3.
Se partono insieme, curva chiusa Come la precedente ma se uno parte a metà percorso dell'altro, curva aperta.

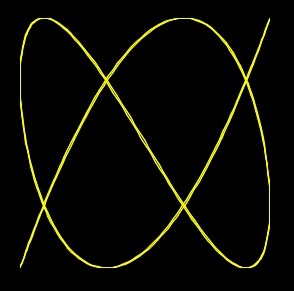
n.13) Sesta Magg. 5:3 chiusa     n.14) Sesta Magg. 5:3 aperta
Nell'intervallo di Quinta, un pendolo compie 4 oscillazioni mentre l'altro ne fa 3.
Se partono insieme, curva chiusa Come la precedente ma se uno parte a metà percorso dell'altro, curva aperta.

n.15) Sesta Magg. 5:3 chiusa     n.16) Sesta Magg. 5:3 aperta
Nell'intervallo di Quinta, un pendolo compie 4 oscillazioni mentre l'altro ne fa 3.
Se partono insieme, curva chiusa Come la precedente ma se uno parte a metà percorso dell'altro, curva aperta.

n.17) Terza Min 6:5 chiusa     n.18)Terza Min 6:5 aperta
Come avrete capito dalle immagini precedenti. Anche queste sopra sono in relazione all'intevallo reciproco, ed al momento del rilascio dell'asta del pendolo.
Nell'immagine a destra, se contate le lunette orizzontali vedrete che sono 6, e le verticali sono 5.
perciò per conoscere gli intervalli delle armoniche, basta contare le lunette orizzontali e verticali.

n.17) Terza Min 8:5 chiusa     n.18)Terza Min 8:5 aperta
Come detto precedentemente per conoscere gli intervalli delle armoniche, basta contare le lunette orizzontali e verticali.
8 orrizontali e 5 verticali

n.19) Spirale     n.20) Doppia spirale
Nella immagine n. 19 vediamo lo smorzamento dei pendoli, quando tracciano l'unisono, vedi l'immagine in alto la num. 2, con il passare del tempo la carica dei pendoli si esaurisce e l'ampiezza delle oscillazioni diminuisce fino a ridursi ad un punto, quando i due pendoli si fermano. Nell'immagine num. 20 abbiamo una doppia spirale ottenuta ruotando e sovvrapponedo il verso delle rotazioni dei pendoli

In questo video potete vedere la simulazione di un armonografo a due pendoli in azione, oltre a vedere come si ottengono le figure viste sopra vedrete come simulando il rilascio graduale dei due pendoli si ottiene l'effetto di un movimento di rotazione che passa da una fase chiusa ad una aperta delle curve.

Armonografo a tre pendoli

Relazione tra le frequenze delle onde sonore di uno strumento musicale e le oscillazioni combinate dei tre pendoli di un Armonografo.
Due dei tre pendoli dell'armonografo oscillano in modo perpendicolare uno all'altro, ossia uno si muove da nord a sud e l'altro da est a ovest.
Il movimento combinato dei due pendoli può produrre delle circonferenze, anche se il terzo pendolo è bloccato, ma se sblocchiamo anche il terzo pendolo, che è agganciato al tavolo in un modo che gli permetta di oscillare a 360 gradi, avremo la somma di due movimenti rotatori che produrrà delle figure molto più elaborate di quelle ottenute con i soli due pendoli a movimento laterale.
Anche in questo caso, mettendo in relazione gli intervalli delle oscillazioni dei tre pendoli potremo creare delle curve che risulteranno più o meno gradevoli visivamente, esattamente come accade con gli intervalli delle note musicali che risultano più gradevoli all'udito se rispettano certi intervalli in rapporti semplici.
Le figure prodotte dai tre pendoli dell'armonografo sono molto più complesse di quelle a due pendoli, e sono in grado di produrre delle figure che si avvicinano a quelle prodotte da un computer con un programma di grafica,
Questo fatto mostra come le onde sonore e le curve prodotte dalle oscillazioni dei pendoli dell'armonografo obbediscano alle stesse leggi matematiche, ed è per questo motivo che un elaboratore elettronico è in grado di riprodurre queste onde, sia in un modo grafico, come i disegni di queste pagine, sia in un modo sonoro ( attraverso midi e strumenti elettronici) suoni che risultano abbastanza simili a quelle degli strumenti musicali non digitali.

img. 1) Unisono. 1:1 discorde     img. 2) Unisono. 1:1 concorde
Img.1) Avremo una diagonale e un movimento discorde, se i due movimenti rotatori hanno la stessa velocità ma le due rotazioni sono contrarie, ossia una va in senso orario mentre l'altra va in senso antiorario.
Img.2)I tre pendoli hanno la stessa velocità, la somma dei due movimenti rotatori produrrà un semplice punto se i due movimenti sono concordi ossia si muovono nella stesso verso.

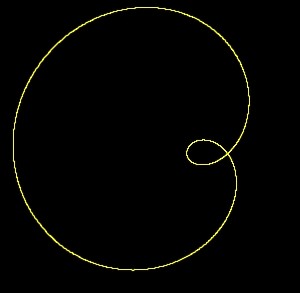
img. 3) Ottava. 2:1 discorde     img. 4) Ottava. 2:1 concorde
Img.3) Una delle due rotazioni ha una velocità doppia ed è discorde, ossia hanno rotazioni contrarie.
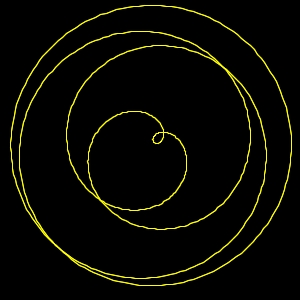
Img. 4) Una delle due rotazioni ha una velocità doppia ed è concorde, ossia hanno rotazioni nello stesso verso

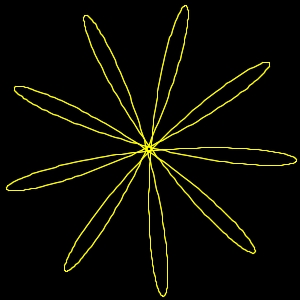
img. 5) Sesta Maggiore. 5:4 discorde     img. 6) Sesta Maggiore. 5:4 concorde
Img.5) Le rotazioni hanno un rapporto 5:4 e sono discordi, verso contrario.
Img.6)Le rotazioni hanno un rapporto 5:4 e sono concordi, ruotano nello stesso verso.

img. 7) Sesta Maggiore 5:3 discorde     img. 8) Sesta Maggiore. 5:3 concorde
Img.7 Le rotazioni hanno un rapporto 5:3 e sono discordi, verso contrario
Img. 8) Le rotazioni hanno un rapporto 5:3 e sono concordi, ruotano nello stesso verso.

img. 9) Terza Maggiore. 5:4 discorde     img. 10) Sesta Maggiore. 5:4 concorde
Img.9) Le rotazioni hanno un rapporto 5:4 e sono discordi, verso contrario.
Img.10)Le rotazioni hanno un rapporto 5:4 e sono concordi, ruotano nello stesso verso.

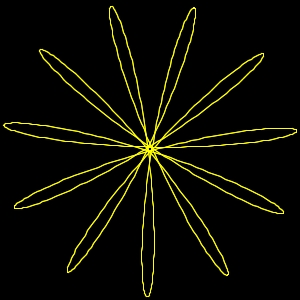
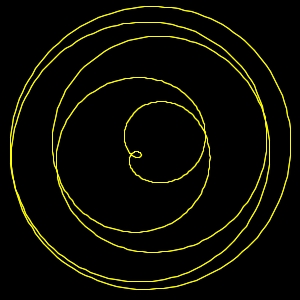
img. 11) Terza Minore 6:5 discorde     img. 12) Terza Minore. 6:5 concorde
Img.11 Le rotazioni hanno un rapporto 6:5 e sono discordi, verso contrario
Img. 12) Le rotazioni hanno un rapporto 6:5 e sono concordi, ruotano nello stesso verso.

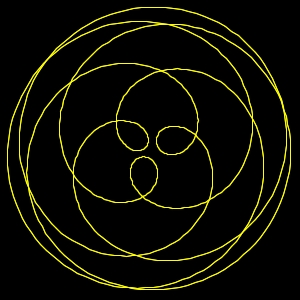
img. 13) Sesta Minore. 8:5 discorde     img. 14) Sesta Minore. 8:5 concorde
Img.13) Le rotazioni hanno un rapporto 5:4 e sono discordi, verso contrario.
Img.14)Le rotazioni hanno un rapporto 5:4 e sono concordi, ruotano nello stesso verso.

img. 15) Tono(sec) 9:8 discorde     img. 16) Tono(sec) 9:8 concorde
Img.15)Le rotazioni hanno un rapporto 9:8 e sono discordi, verso contrario
Img. 16) Le rotazioni hanno un rapporto 9:8 e sono concordi, ruotano nello stesso verso.

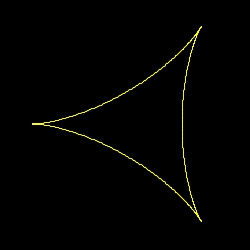
img. 17) Ottava. 2:1 discorde     img. 18) Ottava. 2:1 concorde
Img.17) Le rotazioni hanno un rapporto 8:5 e sono discordi, verso contrario.
Img.18)Le rotazioni hanno un rapporto 8:5 e sono concordi, ruotano nello stesso verso.
Il rapporto e uguale a alle img.3 e img. 4 ma varia l'ampiezza delle rotazioni.

img. 19) Terza Minore. 9:8 discorde     img. 20) Terza Minore. 9:8 concorde
Img.19) Le rotazioni hanno un rapporto 2:1 e sono discordi, verso contrario
Img. 20) Le rotazioni hanno un rapporto 3.2 Lo Stesso discorso per le img. 19 e 20 che sono come le img. 5 e 6. Ma le cui ampiezze vengono invertite, significa che le velocità dei due pendoli con movimento laterale prendono il posto di quello del terzo pendolo, quello con movimento oscillatorio e viceversa.

Tutte queste immagini sono state ottenute con un elaboratore, ho scritto un piccolo programma in modo di simulare facilmente i rapporti delle oscillazioni e le loro ampiezze oltre a variare il tempo di rilascio dei pendoli, e naturalmente inoltre posso variare i colori di ogni oscillazione.

Per vedere veri armonografi in azione o saperne costruire uno, in rete ci sono molti siti, basta cercare con google " armonografo" e troverete molte informazioni.

Questi sono due siti che ho trovato utili per costruire un armonografo a tre pendoli:
https://it.yevgenykafelnikov.com/how-make-three-pendulum-rotary-harmonograph Istruzione per costrire un armonografo a tre pendoli.
https://tech.gnius.it/armonografo-macchina-vi-incanterà filmato istruttivo