Insieme di Mandelbrot pag.2

Come ingrandire un punto dell'immagine dell'insieme di Mandelbrot

Basta ridurre l'estensione del piano complesso da esaminare, normalmente il piano complesso viene esaminato in un'estensione di 2,5 per la parte reale e 2,5 per la parte immaginaria, in pratica la parte reale va da -0.75 a +1.75 e la parte immaginaria da -1.25 a +1.25, Se riduciamo l'estensione a 0.025 per la parte reale e 0.025 per la parte immaginaria, abbiamo un ingrandimento di 100 volte e potremmo vedere più dettagli di un punto dell'immagine, ma poichè si può ridurre l'estensione del piano complesso fino a 0.00000000001 (anche di più, dipende dalla potenza di calcolo dell'elaboratore ) sia per la parte reale e per la parte immaginaria, puoi immaginare il numero d'ingrandimenti possibili.
Ma la cosa incredibile è che molte zone dell'immagine originale se sottoposte a ingrandimento mostrano sempre la stessa struttura un' infinità di volte, sempre un insieme di Mandelbrot, magari leggermente ruotato o spostato, ma sempre simile all'originale.

Qui di seguito si può vedere un esempio di questi ingrandimentiè.

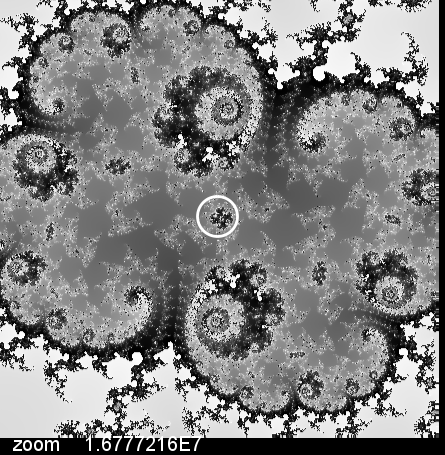
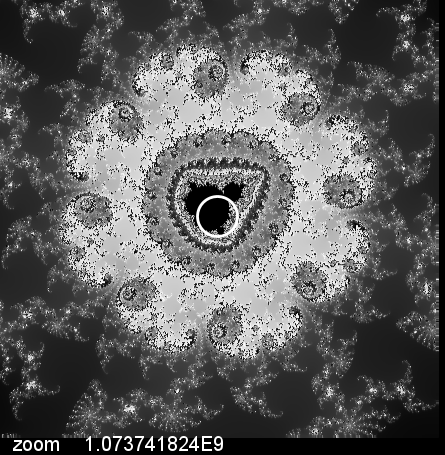
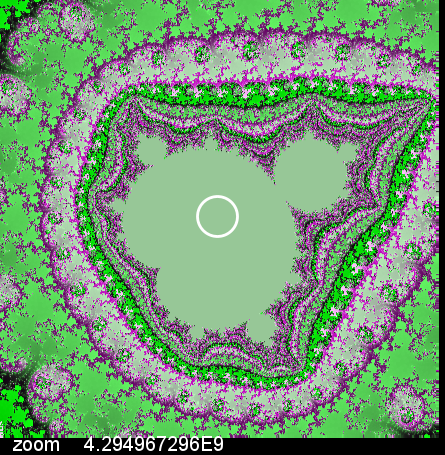
Come si può vedere, abbiamo uno zoom che supera i 4 miliardi, nota anche che il punto scelto per lo zoom si trova in una zona dell'immagine molto vicina al bordo, perchè è la zona che mostra più dettagli e dove è più facile imbattersi in altre copie dell'insieme di Mandelbrot.



Per quste immagini sopra ho seguito un prcorso inusuale, sono partito da un punto
dell'insieme di M. con uno zoom elevato e lentamamento sono tornato all'immagine di partenza con zoom = 1.


Queste sotto sono immagini ottenute con un altro metodo, ho utizzato il numero dei cicli utilizzati dall'algoritmo per calcolare se il pixel in esame apparteneva o meno all'insieme di Mandelbrot, ad esempio se il numero dei cicli è 100, il pixel viene colorato con un colore diverso da quello di un pixel che ha richiesto 200 cicli per essere calcolato, in questo modo si ottiene un'immagine molto colorata e bella da vedere, perchè ad ogni ciclo viene associato un colore diverso.
Ma oltre al colore ho utilizzato il numero dei cicli per creare delle immagini che mostrano un effetto tridimensionale in pratica più il numero dei cicli utilizzati dall'algoritmo è elevato più il pixel viene spostato verso l'alto,


Come puoi verdere i punti più in alto dell'immagine qui sopra hanno colori differemti uno dall'altro,
questo perchè il numero dei cicli utilizzati da questi pixels è molto vicino al numero massimo di cicli che l'algoritmo può utilizzare, per decidere se il pixel in esame appartiene o meno all'insieme di Mandelbrot, che come sappiamo non deve superare la dimensione di 2, quindi se il pixel in esame supera questo valore non appartiene all'insieme di Mandelbrot e qundi il pixel viene colorato in base al numero di cicli utilizzati dall'algoritmo, ma se il numero massimo dei cicli messi a disposizione dal programma è 1000 e dopo tale numero il pixel in esame non ha superato il valore di 2, allora appartiene all'insieme di Mandelbrot e di solito viene colorato con il colore nero o con un colore scuro.


Come si vede dall'immagine qui sopra più ci si allontana dalla parte colorata di nero, più velocemente si supera la dimensione di 2 e servono pochi cicli per stabilire che il pixel in esame non appartiene all'insieme di M.
in questa e nelle due immagini seguenti ho aggiunto un altro insieme di Mandelbrot colorato di marroncino per esaltare l'effetto tridimensionale ed evidenziarne il confine.

Questo filmato è un' animazione tridimensionale dell'insieme di Mandelbrot che evidenzia come il bordo dell'insieme richieda un numero di cicli molto maggiore per determinare se il pixel in esame appartiene o meno all'insieme di Mandelbrot,

In questa filmato per semplice curiostà ho spalmato un insieme di Mandelbrot su una mezza sfera.

Aumentare il valore della potenza della formula Z^2 +c

Si può anche aumentare il numero della potenza della formula che genera l'insieme di Mandelbrot, in questo caso la formula diventa:

Z^3 +c oppure Z^4 +c oppure Z^n +C

con n che può variare da 2 a 20 o maggiore, ma in questo caso l'immagine che si ottiene è molto diversa da quella dell'insieme di Mandelbrot originale, ma comunque sempre molto bella e interessante.

Qui di seguito si possono vedere alcuni esempi di immagini ottenute con potenza 3, 4, 5, 6 e 7

Sono immagini colorate in modo da esaltare i valori di (n) della formula











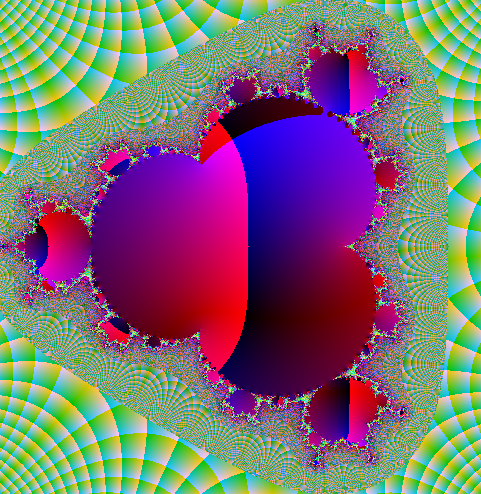
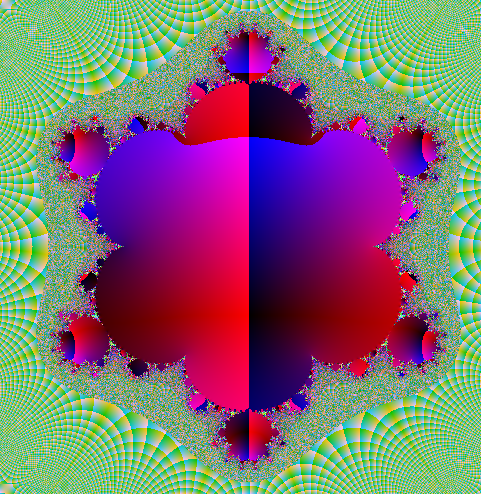
Queste sotto sono immagini ottenute con potenza 3, 4, 5, 6, 7, 8, 12 e 16, con alcuni ingrandimenti.




Questa sopra mostra una zona leggermente ingrandita dell'immagine precedente

Qui sotto mostro due ingrandimenti diversi della stessa immagine, nota il valore di zoom.




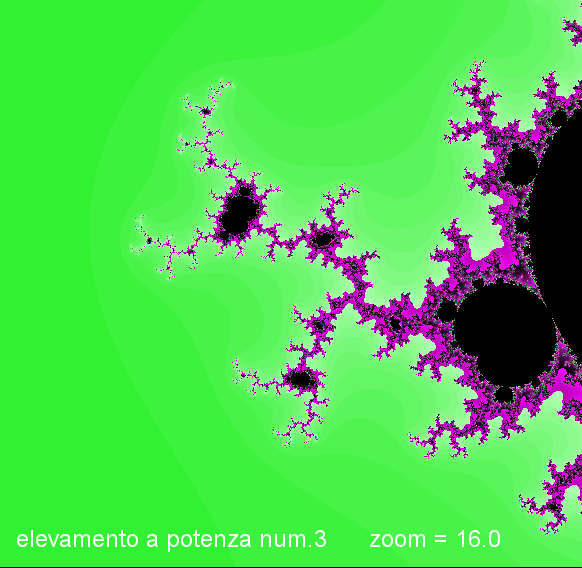
immagine sotto con N= 4


qui sotto n = 5


qui sotto due immagini con n= 5 e zoom differenti




qui sotto N =6


qui sotto N =7


qui sotto N =8






Qui sopra abbiamo N = 12,
mentre qui sotto abbiamo sempre N =12 ma con un ingrandimento di un punto del bordo abbastanza elevato, come puoi vedere alcuni punti del bordo se ingranditi presentano sempre uno schema simile anche con valori di N diversi
nota il valore di zoom


qui sotto N =16





Come si può vedere, dopo un certo valore di N l'immagine diventa molto simile a quella precedente.


Qui sotto potete vedere tre immagni realizzate modificando leggermente l'algoritmo dell'insieme di Mandelbrot


Sembrano strani maggiolini


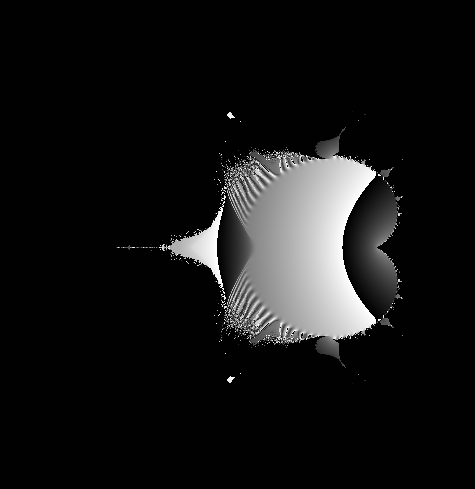
Mi ha sorpreso come una semplice formula matematica abbinata alla potenza di calcolo di un modesto elaboratore possa generare tante immagini interessanti