Insieme di Mandelbrot pag.1

Cominciamo con la formula matematica che permette di relizzare l'insieme di Mandelbrot

LA FORMULA e' Z = (Z^2 + c)

Dove Z e c sono numeri complessi. Come vedi la formula che si deve reiterare è molto semplice, ed ha praticamente solo due passaggi.

(1) un numero complesso (Z) si eleva al quadrato.
(2) Poi si somma un altro numero complesso (c).

Questi 2 passaggi si ripetono per un numero di volte che può variare da 40 a 10.000 volte, poi vedremo perchè.

I numeri complessi, sono composti da due parti, una detta reale e una detta immaginaria, un esempio di numero complesso è questo 2 +3i dove 2 rappresenta la parte reale e +3i rappresenta la parte immaginaria, anche se di immaginario non ha niente, vediamo subito a cosa servono i numeri complessi.
Questi numeri, servono ad individuare un punto sul piano.

>

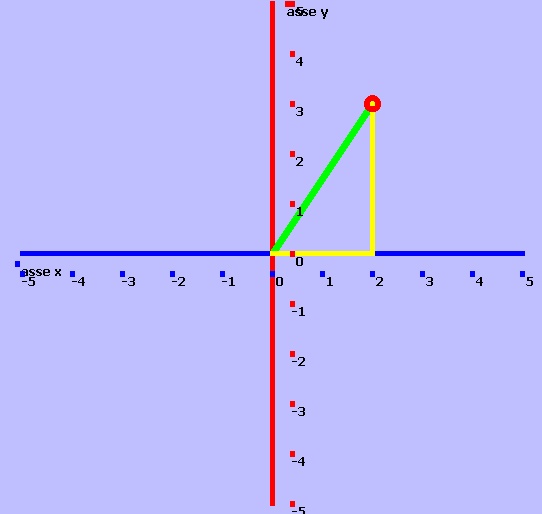
Il piano e i numeri complessi

Come vedi dal disegno, il piano complesso è un piano bidimensionale con origine nel centro.
I numeri della riga orizzontale in blu, rappresentano la parte reale del numero complesso, a destra dello zero sono positivi, a sinistra dello zero sono negativi,
I numeri della riga verticale in rosso rappresentano la parte immaginaria del numero complesso, quelli sopra lo zero sono positivi, quelli sotto sono negativi.

Perciò il cerchietto rosso corrisponde al numero complesso 2 +3i, perchè è 2 numeri a destra dello zero e 3 numeri sopra lo zero centrale.

Altra cosa molto importante da sapere è la DIMENSIONE del numero complesso, per dimensione intendiamo la distanza dal punto centrale del piano,
la distanza è in pratica l'ipotenusa del triangolo che si forma congiungendo il punto della parte reale(2) con il punto della parte immaginaria(+3i) con l'origine del piano,
perciò la dimensione di un numero complesso è LA RADICE QUADRATA della somma dei quadrati dei numeri reali ed immaginario.
La dimensione di 2 +3i è la radice quadrata di (4 + 9) cioè 3,605 circa.

La dimensione è molto importante, perchè i numeri che appartengono
all'insieme di Mandelbrot Sono solo quelli che non superano la dimensione di 2 .

Ora che sappiamo cosa sono il piano complesso e i suoi numeri

Vediamo la regione del piano complesso che c'interessa.

Coordinate

I numeri che c'interessano, come si vede dall'immagine vanno dal numero    -2 al numero   +0,5  

Occupano perciò un'estensione pari a 2,5 per la parte reale,(La riga rossa)

Mentre vanno dall'1,25    al    -1,25   per la parte immaginaria,perciò sempre 2,5.

(La riga verticale verde)
La metà superiore allo zero del piano, è un'immagine speculare di quella inferiore, anche a forti ingrandimenti, si vedrebbero gli stessi particolari ma invertiti.

C'interessa solo questa estensione di   2,5  perchè è la sola zona ad evidenziare la bellezza del disegno, non appena si supera questa estensione, il numero dei cicli utilizzati dalla formula per superare la dimensione di   2    ( la dimensione in questo caso è la lunghezza dell'ipotenusa vista prima) sono molto simili, e poichè il colore del disegno è scelto in base al numero dei cicli è se i cicli sono simili il disegno diventerebbe monotono.
  Ci sono certi numeri che riescono a superare la dimensione di   2   in 20 cicli, ovvero la formula viene ripetuta 20 volte prima di superare la dimensione di   2,   altri numeri impiegano 50 cicli, ebbene il colore delle immagini che vedi in queste pagine, dipende dal numero di cicli impiegati a superare la dimensione di   2. 

Ogni pixel dell'immagine, corrisponde ad un punto del piano complesso, perciò per ottenere un' immagine è bastato mettere in relazione un pixel del monitor, con il numero corrispondente al piano complesso, (trasformare cioè lo schermo del computer in un piano complesso), sottoporre ogni pixel alla formula di Mandelbrot e colorarlo in base alla velocità impiegata a superare la dimensione di  2,
Nell'immagine sopra,(quella con le coordinate,) i numeri che impiegavano meno tempo a superare la dimesione di  2  li ho colorati di grigio, e di verdeazzurro, quelli lentissimi di bianco, infine quelli che appartenevano all'insieme di Mandelbrot, non riuscivano cioè a superare la dimensione di  2 nemmeno dopo numerosi cicli, li ho colorati di nero.

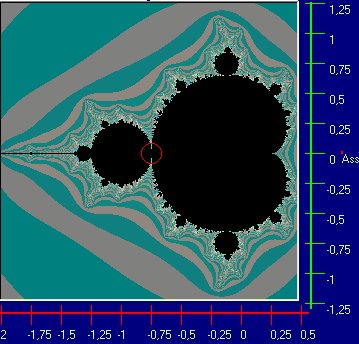
La zona che nasconde le immagini più spettacolari e quella colorata che confina con il bordo nero all'interno del disegno.

Nell'immagine qui a fianco si vede meglio la zona dove si nascondono i motivi più interessanti.
E' quella più interessante, perchè è la zona di confine tra i numeri che appartengono all'insieme di Mandelbrot ossia quelli neri, che non superano mai la dimensione di   2    e quelli che appartengono all'altro gruppo, quelli che superano la dimensione di 2

Tra questi ci sono quelli che potremmo chiamare gli indecisi, impiegano cioè molto tempo(cicli) a decidersi se stare tra i neri, o i colorati, sembrano attratti dal mondo nero, ma poi alla fine si decidono e passano in quello colorato.
Questi indecisi si trovano nella zona di confine dei due insiemi, la zona che nell' immagine qui sopra appare colorata.
A forti ingrandimenti,questa loro indeciosione aumenta di molto , e può durare fino a  1.000 cicli,

Pensate per decidere il colore di un singolo pixel bisogna ripetere la formula di Mandelbrot anche 1000 volte, ma il risultato produce immagini sorprendenti.