Equazioni diofantee
e terne pitagoriche
Cominciamo da Pitagora matematico greco nato a Samo nel 575 a.C. che con il suo teorema stabilisce una relazione tra i lati di un triangolo rettangolo, il teorema dice che la somma dei quadrati dei due cateti è uguale alla somma del quadrato dell'ipotenusa a² +b²= c²
Dopo questa scoperta molti cercarono di scoprire un modo semplice per ottenere altre terne formate solo da numeri interi, perchè 3²+ 5²= 34 e non c'è un numero intero che elevato al quadrato dia 34.
Naturalmente molti matematici sapevano partendo da una terna pitagorica tipo 3²+ 4²,= 5² si poteva ottenerne molte altre, bastava moltiplicare per un numero naturale qualsiasi i tre valori iniziali, ad esempio moltiplicando per 2 i numeri della terna 3, 4 e 5, abbiamo 6²+ 8²=10² ma non si conosceva una formula per trovare delle terne primitive, una terna pitagorica è primitiva solo se i tre valori a, b e c non hanno divisori comuni, 
A quanto si sà solo dal 3º secolo avanti Cristo, Euclide ed altri matematici del tempo cominciarono ad usare le seguenti formule per trovare le terne pitagoriche con numeri naturali .
a= (m²-n²), b= (2*m*n), c= (m²+n²)
dove (n) e (m) sono rispettivamente il numeratore e il denominatore (n/m) di una frazione, tipo ½, ¼, ¾.
Da notare che se (n) e (m) sono entrambi dispari, a, b e c risulteranno pari, e quindi quella terna non potrà essere primitiva.
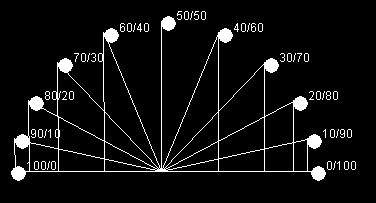
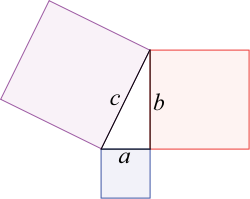
Oltre a dimostrare che le terne pitagoriche sono infinite, queste formule risolvevano due problemi, primo, trovare facilmente molte terne primitive, secondo, quello di trovare un triangolo rettangolo con il cateto verticale, che fosse una determinata frazione della somma dell'ipotenusa con il cateto orizzontale, nella figura qui sopra, (b) è una frazione di (a+c).
Ad esempio vogliamo che il lato (b) sia lungo la metà, della somma de lato minore (a) con l'ipotenusa (c).
La metà di qualcosa è 1/2 e noi mettiamo il numeratore (n= 1) e il denominatore (m= 2)
abbiamo così lato a= (m²=4) e (n²=1)= (4-1)=3
poi abbiamo lato b= (2*m*n)= (2*2*1)= 4
infine ipotenusa c= (m²=4) e (n²=1)= (4+1)=5
Ecco che oltre alla terna di numeri interi abbiamo anche la dimostrazione che il lato (b)=4 è uguale alla metà(½) della somma del lato (a) con l'ipotenusa (c), a+c =8
Facciamo un secondo esempio
Vogliamo che il lato (b) sia lungo ¼ della somma de lato (a) con l'ipotenusa (c).
Un quarto di qualcosa si scrive 1/4 e noi mettiamo il numeratore (n= 1) e il denominatore (m= 4)
abbiamo così lato a= (m²=16) e (n²=1)= (16-1)=15
lato b= (2*m*n)= (2*4*1)= 8
infine ipotenusa c= (m²=16) e (n²=1)= (16+1)=17
Ecco che il lato (b)=8 è uguale un quarto (¼) della somma del lato (a) con l'ipotenusa (c), a+c =32
Nota che il valore del cateto orrizontale (a) si può ottenere anche così (m+n)x(m-n) ad esempio con (m=4) e (n=1) si fa così (4+1)x(4-1)= 15
Oppure quando la differenza tra (m) e (n) è uguale a 1 come ad esempio 1/2 basta sommare (m) con (n) 2+1= 3, con 3/4 abbiamo 4+3= 7 etc.
Inoltre
a² = (c - b)*(c + b)
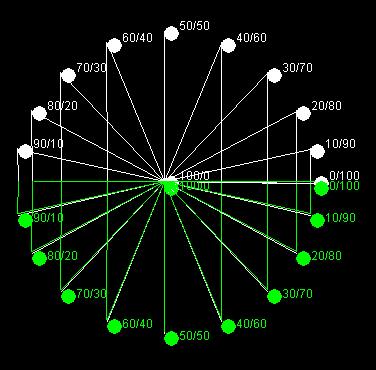
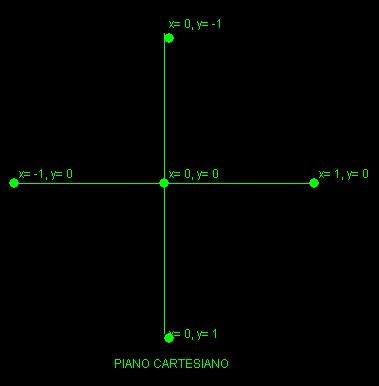
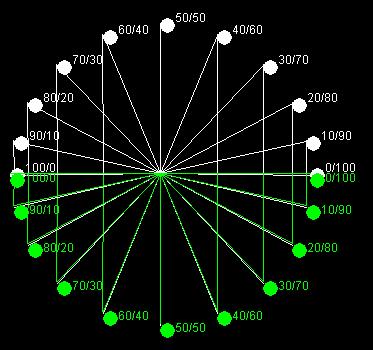
Nel 3º secolo dopo Cristo perciò sei secoli dopo Euclide, Diofanto, che viveva in Alessandria d'Egitto ma era un matematico greco, lavorando con le frazioni scoprì che dividendo (a per c) e (b per c) trovava due valori, x e y e sommandone poi i quadrati otteneva sempre il numero 1.
(a/c)=x
(b/c)=y
(x²+y²) = 1
infine ottenne una formula per risolvere un equazione chiamate ancora oggi
EQUAZIONE DIOFANTEA (o anche equazione diofantina)
X²+Y²= 1
dove
X= (1-t²)/(1+t²)
y= (2+t)/(1+t²)
dove (t) = n/m
n ed m sono il numeratore ed il denominatore di una frazione
Facciamo un esempio con t = 1/2
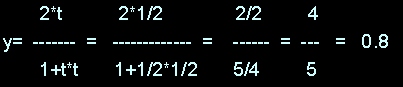
0.36 + 0.64 = 1
Abbiamo x= 3/5, y= 4/5 se togliamo il denominatore otteniamo x=3 e y=4 e se mettiamo z=5 che è il valore del denominatore, abbiamo gli stessi valori di (a),(b),(c) delle terne pitagoriche di Euclide che abbiamo visto all'inizio
Se poi si divide x/z e y/z otteniamo rispettivamente 0.6 e 0.8, infine sommiamo il quadrato di questi 2 valori ed abbiamo 0.36+ 0.64 = 1
x corrisponde al valore del cateto orrizontale, mentre y a quello del cateto verticale, perciò x²+y²=1
Nota che y= 0.8 è uguale ad 1/2 di 1.6 che corrisponde alla somma di (x+z) = (0.6 + 1= 1.6)
Facciamo un altro esempio con t = 3/4
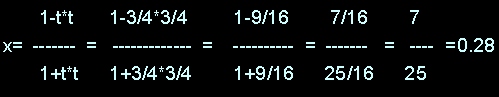
Abbiamo rispettivamente x= 7 y=24 e z= 25
Ossia 25+7= 32 e 24 che corrisponde a 3/4 di 32
e 0.28²+0.96²= 1
Diofanto però non si pose il problema se la sua Equazione desse tutte le soluzioni razionali, solo tra il X e XI secolo dopo Cristo i matematici arabi scoprirono che la formula Diofantea X²+y² =1 ha un eccezione, non funziona quando X= -1 e Y= 0, perchè per avere Y = 0 dobbiamo avere (t = 0), ma in questo modo X non può assumere il valore di -1.
Infine è solo tra il XVI e il XVII secolo con il piano cartesiano di René Descartes nato in Francia nel 1649 italianizzato con Cartesio, che viene collegata questa equazione alla sua rappresentazione nel piano, dove i suoi punti formano una circonferenza di raggio 1.
Qui sotto ho reso graficamente alcuni valori di questa equazione.
Dato che una circonferenza di raggio 1 è praticamente invisibile ho moltiplicato il raggio (che corrisponde all'ipotenusa dei triangoli) e i valori di x,y (rispettivamente il cateto orrizontale e verticale) per 150.
I numeri corrispondono ai valori di t(10/90, 20/80 etc) mentre le posizioni dei pallini corrispondono alle coordinate dei valori di (x,y) nel piano cartesiano.
A conferma dell' eccezione che dice :- L'equazione non funzione con x=-1 e y=0.
Notate che con (t = 100/0) il triangolo non si completa ed il pallino si posiziona nel punto d'origine del piano, cioè x=0, y=0,
Notate ancora anche che per avere la rappresentazione di metà circonferenza il valore di (t) passa (100/0) a (0/100) ossia il denominatore va da 0 a 100 mentre in numeratore passa da 100 a 0, quando numeratore e denominatore assumono lo stesso valore si arriva a 1/4 di circonferenza, per avere la rappresentazione dell'intera circonferenza ho mantenuto i valori delle ascisse (x) e invertito le coordinate di (y)
Accanto potete vedere una rappresentazione del piano cartesiano
cateti verticale = coordinate y
cateti orrizontale = coordinate x
ipotenusa = raggio del cerchio.
A differenza dell'equazione diofontea, con le formule euclidee si può ottenere anche la coordinata x=-1, y=0
Qui sopra a sinistra abbiamo un altro esempio di una rappresentazione di terne pitagoriche nel piano cartesiano,
questa volta i triangoli sono ottenuti utilizzando le formule Euclidee viste all'inizio, nella prima immagine a sinistra abbiamo un valore (n) che rimane fisso a 100, mentre (m) aumenta di ogni volta di 10, abbiamo 100/0, 100/10, 100/20, 100/30 etc. questa immagine mostra che quando numeratore e denominatore sono uguali abbiamo x=0 e y=1 oppure y= -1
Nell'immagine a destra i valori di (n)e (m) cambiano contemporaneamente, 100/0, 90/10, 80/20 etc.
Nota che quando n/m è uguale 50/50 ossia abbiamo il cateto verticale che è uguale alla somma del cateto orrizontale con l'ipotenusa, del relativo triangolo si vede solo l'ipotenusa, poichè l'ipotenusa per forza di cose è uguale al raggio della circonferenza ne consegue che il lato(a= cateto orrizontale ) è uguale a zero ed il lato(b= cateto verticale) è uguale all'ipotenusa, che in questo modo lo copre, nascondendolo.
Abbiamo visto che con le formule euclidee abbiamo (a= m²-n²) e (b= 2*m*n) mentre (c=m²+b²).
Con (a/c) abbiamo i valori di(x), mentre con (b/c) abbiamo i valori di (y).
Qui sopra a destra si vedono i valori di (x,y) nel piano cartesiano.
Sommando poi i quadrati abbiamo, (x²)+(y²) = 1.
Perciò con le formule euclidee si possono ottenere anche i valori di x=-1 y=0.
Facciamo un esempio, se poniamo (m=0) e (n=10).
abbiamo a= (0²-10²= -100).
poi b=(2*n*m)= 0
infine c=(m²+n²)100
Perciò x= a/c = -100/100 = -1
y = b/c = 0/100= 0.