Le radici di un numero

Questo metodo, parte da una congettura iniziale e procede attraverso una successione di approsimazioni sempre migliori, fino a giungere ad un punto stazionario.
Un breve esempio per chi non conosce il metodo di Newton per trovare la radice quadrata di un numero.
Se vuoi trovare la radice quadrata di 11 , puoi partire dal numero 3 ma il suo quadrato 9 è minore di 11, perciò puoi provare con il numero 4, il suo quadrato è 16, maggiore di 11, perciò puoi provare con il numero 3.5 con il suo quadrato di 12.25 è ancora maggiore di 11, vai avanti in questo modo fino a trovare il numero che elevato al quadrato è uguale a 11.
Userò questo metodo, ma con i numeri complessi per trovare la radice di un numero complesso.

La cosa interessante è che il metodo di Newton, non solo permette di trovare la radice quadrata di un numero, ma anche la radice a quadrata di un numero complesso, e non solo, ma anche la radice cubica, la radice quarta, ecc.
Perciò il metodo di Newton è un metodo che permette di trovare le radici di un polinomio di qualsiasi grado.
Grazie alla velocità di calcolo del calcolatore, questo metodo permette di realizzare immagini grafiche sorprendenti.

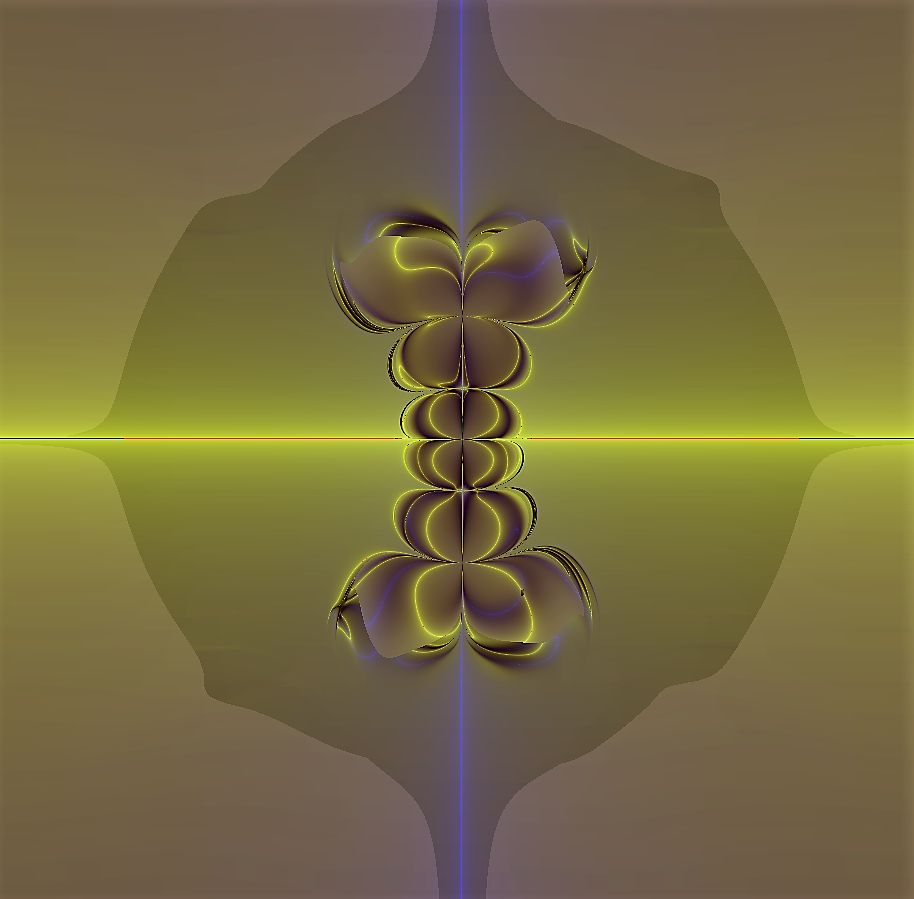
L'immagine qui sopra, ha un'estensione nel piano complesso, che va da -2 a +2 sia per la parte reale, che per la parte immaginaria del piano complesso.
çe due radici quadrate sono 1 e -1, che sono i puntini bianchi al centtro di quelli che dembrano due occhi.
Nei numeri reali la radice quadrata, cubica, quarta, quinta etc. di 1 è sempre = 1 e -1.

Aanche nel piano complesso la radice quadrata di 1 è 1 e -1, ma la radice cubica ha tre soluzioni che sono
1, -0.5 + 0.866i e -0.5 - 0.866i.
La i che vedi dopo il numero 0.866 indica la parte immaginaria del numero complesso.
La radice quarta ha 4 soluzioni che sono
1, i, -1 e -i.
La radice quinta ha 5 soluzioni che sono
1, 0.309 + 0.951i, -0.809 + 0.588i, -0.809 - 0.588i e 0.309 - 0.951i.
Ossia ogni ennesima radice ha n soluzioni, che sono i vertici di un poligono regolare inscritto in un cerchio

Ho unito i punti che corrispondono alle tre radici cubiche ottenendo un triangolo equilatero.

I numeri complessi, sono composti da due parti, una detta reale e una detta immaginaria, un esempio di numero complesso è questo -0.5 +0.866i dove 0.5 rappresenta la parte reale ossia la parte orrizzontale del piano e +0.866i rappresenta la parte immaginaria, vale a dire la parte verticale del piano, vediamo subito a cosa servono i numeri complessi.
Questi numeri, servono ad individuare un punto sul piano.
nell'immagine qui sopra una delle tre radici cubiche di 1 si trova a -0.5 +0.866i
Significa a -0.5 a sinistra dello zero che corrisponde al centro del triangolo e a +0.866 sopra lo zero.
la seconda radice si trova sempre a -0.5 a sinistra dello zero, ma conla parte immaginaria questa volta è sotto lo zero = -0.866i
La terza radice è = 1 +0i
ossia 1 a destra dello zero e la parte immaginaria = 0.i di solito viene omessa, perchè è sottinteso che è l'altezza zero del piano.
Come vedi le tre radici sono al centro di quelli che sembrano tre occhi
elevando al cubo ognuno di questi 3 numeri complessi otterrai sempre 1
Otterrai sempre questi numeri
anche con le 6 radici seste di 1 che formano un esagono
oppure con le 12 radici dodicesime che formano un dodecagono anche se alcuni numeri si scambiano di posto ossia 0.5 diventa 0.5i e 0.866i diventa 0.866 reale

In queste 5 immagini seguente, ho colorato con tonalità diverse, ogni zona appartenente a ciascuna delle tre radici. In questo modo posso mostrarvi alcuni particolari interessanti.

>
per mostrare alcuni particolari interessanti. Nota il comportamento frattale dei confini delle tre radici.

Ingrandendo i confini si vede il ripetersi dello stesso disegno.

Un'altra cosa interessante è l'andamento dei colori dei tre confini .

Lungo i l confine di ogni radice, sembra che l'algoritmo abbia delle difficoltà a decidere dove posizionare il suo colore di appartenenza.

Il rosa si scambia con il verde ed il verde con il blu.

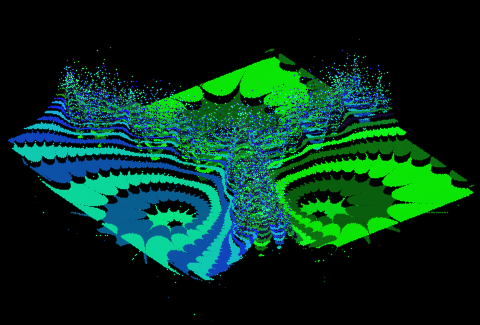
In questa immagine ho alzato i punti di confine in base al numero di cicli usati dal programma per decidere per quale radice optare.

Come per l'immagine precedente il numero dei cicli usati ne determina l'altezza.

Questi evidenziati sono i confini delle quattro radici quarte dl'imagine qui sotto

Le quattro radici quarte sono nel centro dei quattro punti stellati, e si trovano a.
-1:-1i: 1: 1i

Qui vediamo le 5 radici quinte.