Insieme di Julia

Cominciamo con la formula matematica che permette di relizzare l'insieme di Julia

LA FORMULA è Z = (Z² + c)

Dove Z e c sono numeri complessi. Come vedi la formula che si deve reiterare è molto semplice, ed ha praticamente solo due passaggi.

(1) un numero complesso (Z) si eleva al quadrato.
(2) Poi si somma un altro numero complesso (c).

Questi 2 passaggi si ripetono per un numero di volte che può variare da 40 a 10.000 volte, poi vedremo perchè.

Se avete visto la pagina iniziale dell'insieme di Mandelbrot avrete notato che la formula è praticamente la stessa,
ma con una differenza, in questo caso nel numero complesso, la parte (c) della formula Z²+c è fissato su di un valore corrispondente ad un determinato punto del piano complesso, mentre in Mandelbrot abbiamo sempre valori differenti per ogni coordinata del piano corrispondente a "c", per questo motivo ogni punto del piano appartenente all'insieme di Mandelbrot può essere utilizzato per ottenere un insieme di Julia.

>

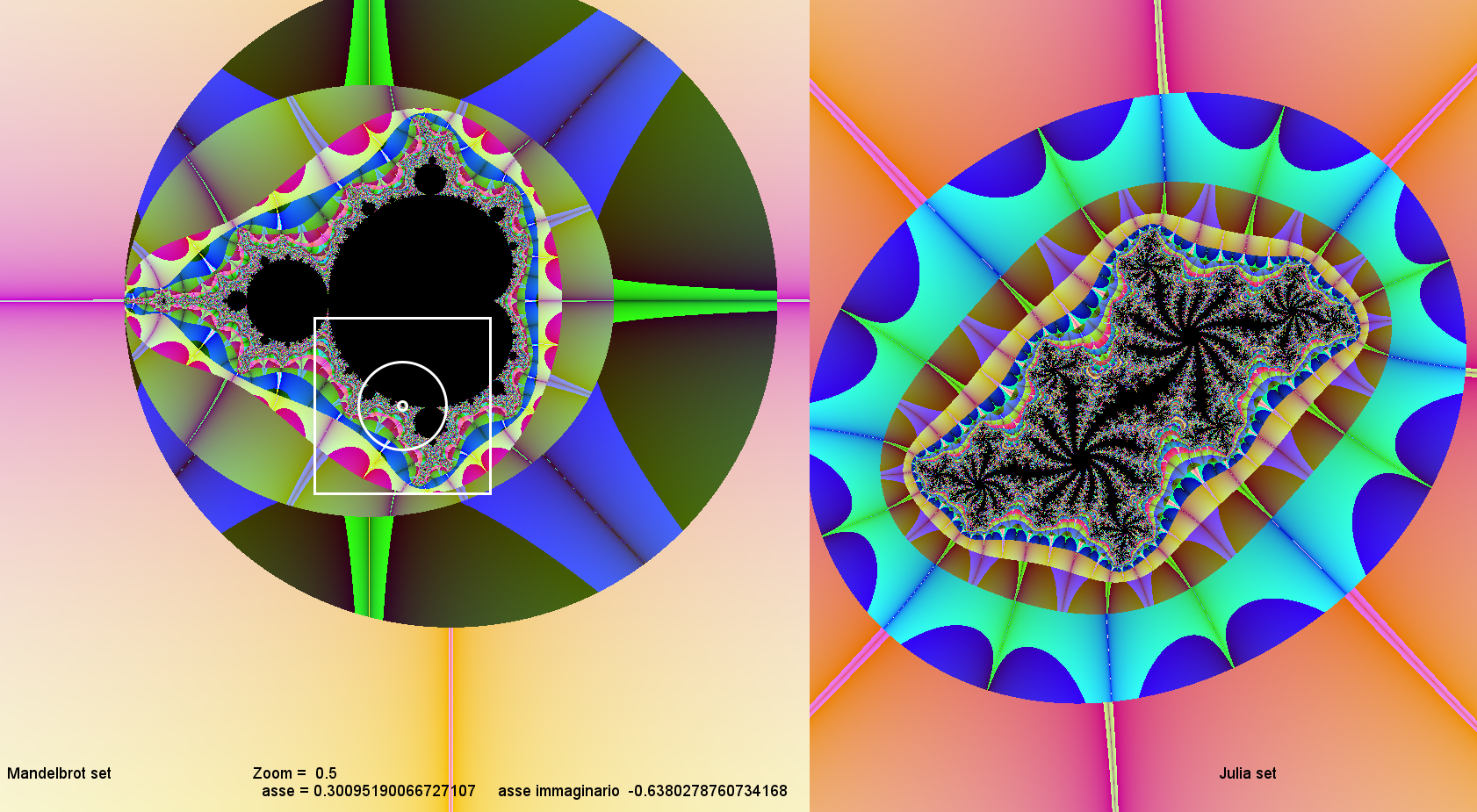
Qui sopra abbiamo l'insieme di Mandelbrot con un cerchietto, Il centro del cerchietto corrisponde al punto c della formula Z²+c dell'insieme di Julia.
Conseguentemente ogni coordinata dell'insieme di Mandelbrot può fornire un'immagine dell'insieme di Julia.

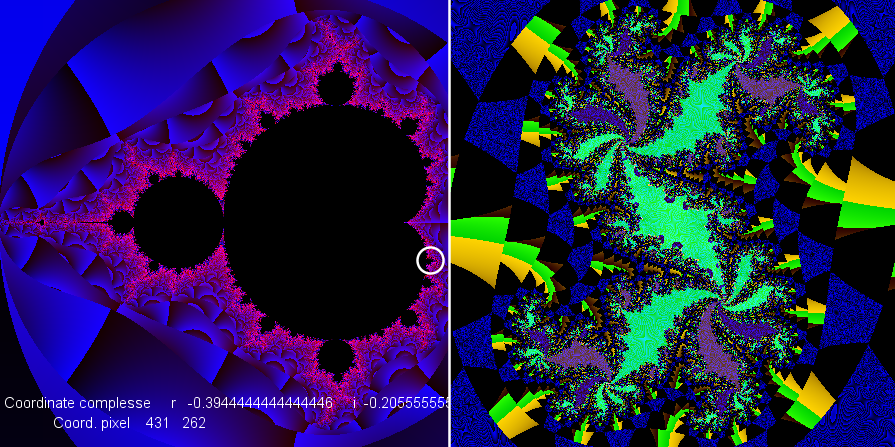
Questa sotto è l'immagine dell'insieme di Julia corrispondente al centro del cerchietto che appare nell'insieme di Mandelbrot a sinistra, in basso a sinistra ho registrato le coordinate del centro del cerchietto.

>

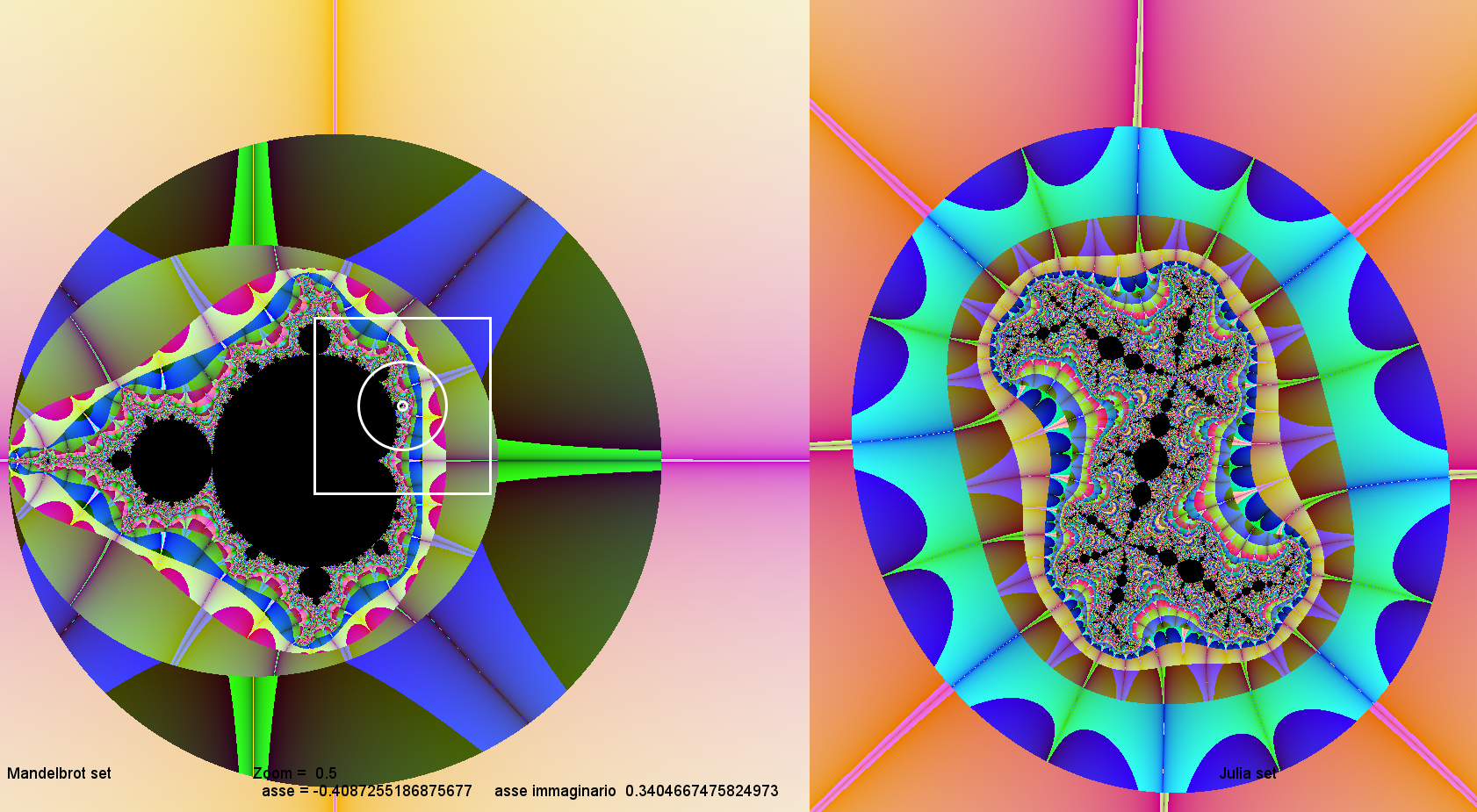
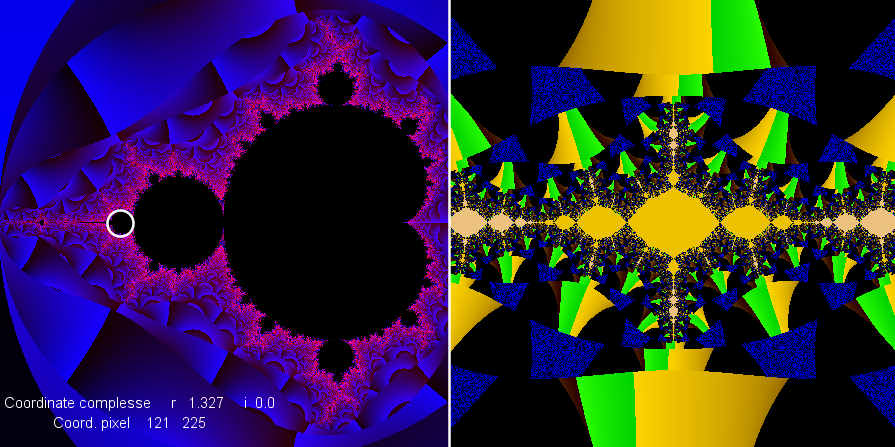
Questa sotto è un'altra immagine dell'insieme di Julia sempre corrispondente al centro del cerchietto che appare nell'insieme di Mandelbrot a sinistra.

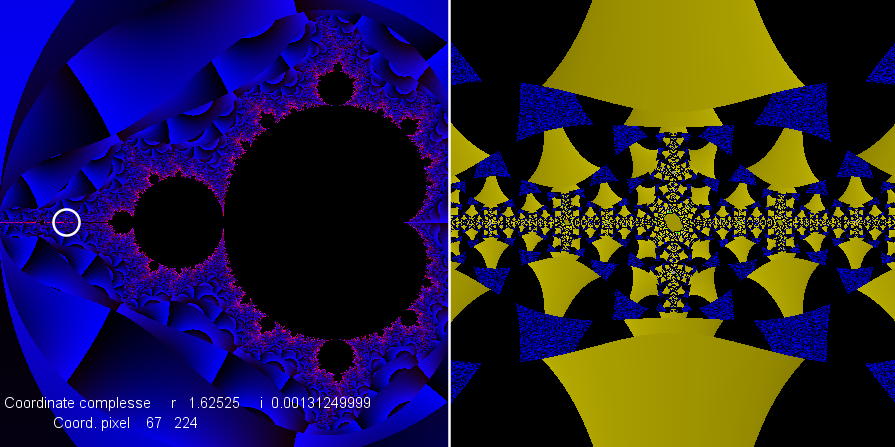
Come si può vedere le immagini migliori dell'insieme di Julia corrispondono ai punti del piano che confinano con il bordo nero dell'insieme di Mandelbrot

>

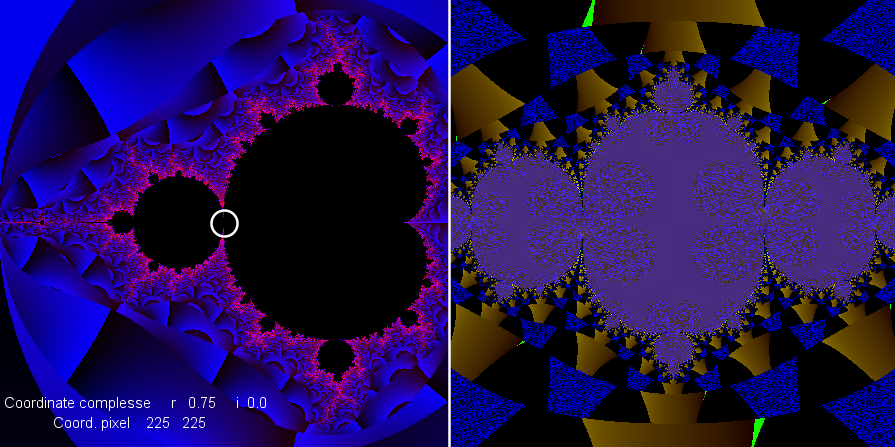
Di seguito alcune altre immagini che mostrano la grande varietà di immagini dell'insieme di Julia.

>

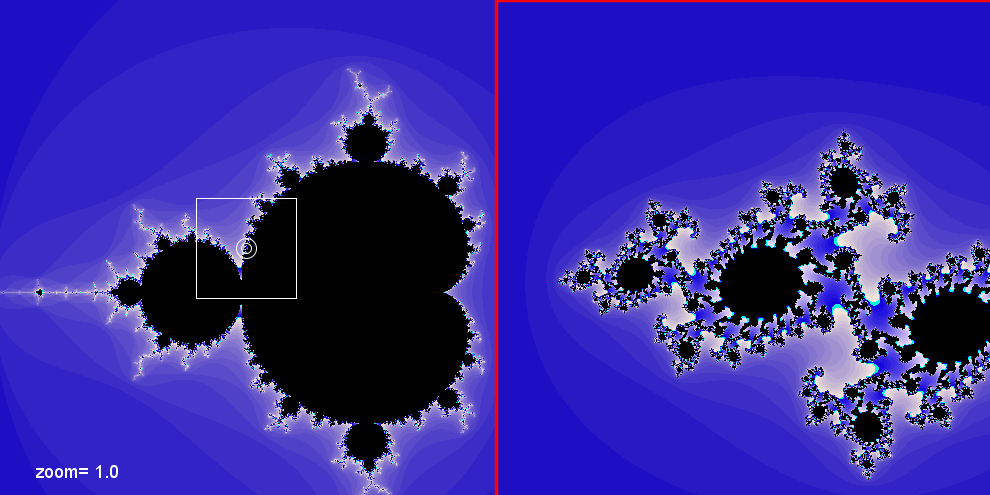
Anche aumentando gli ingrandimenti si possono ottenere immagini di Julia interessanti.

>

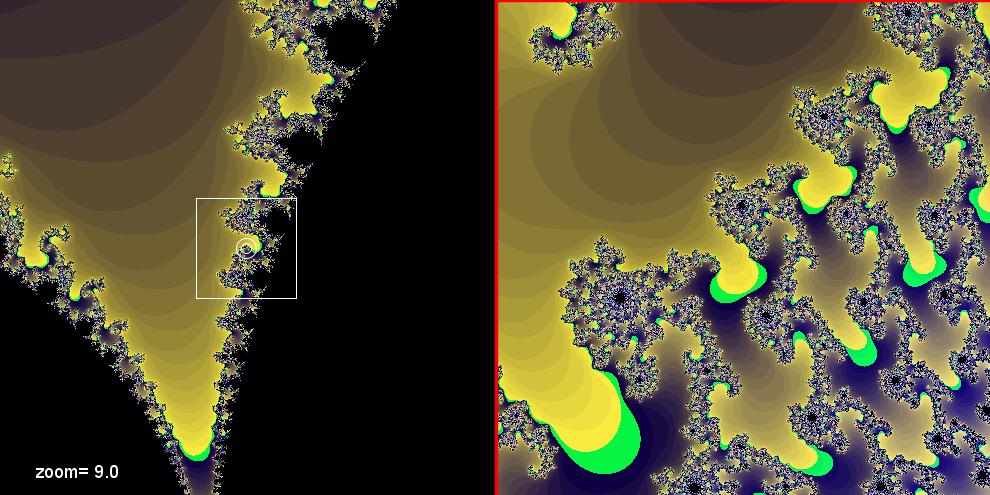
Come ho detto ad ogni coordinata dell'insieme di Mandelbrot corrisponde un insieme di julia diverso, ma la cosa strana, è che se all'inizio abbiamo un diverso insieme di Julia per ogni coordinata dell'insieme di Mandelbrot, quando andiamo ad ingrandire le immagini dei due insiemi, scopriremo, che come si vede dagli esempi seguenti, all'aumentare degli ingrandimenti le differenze dei due insiemi diminuiscono progressivamente fino a far sembrare le due immagini molto simili, quando si raggiungono certi ingrandimenti.

>

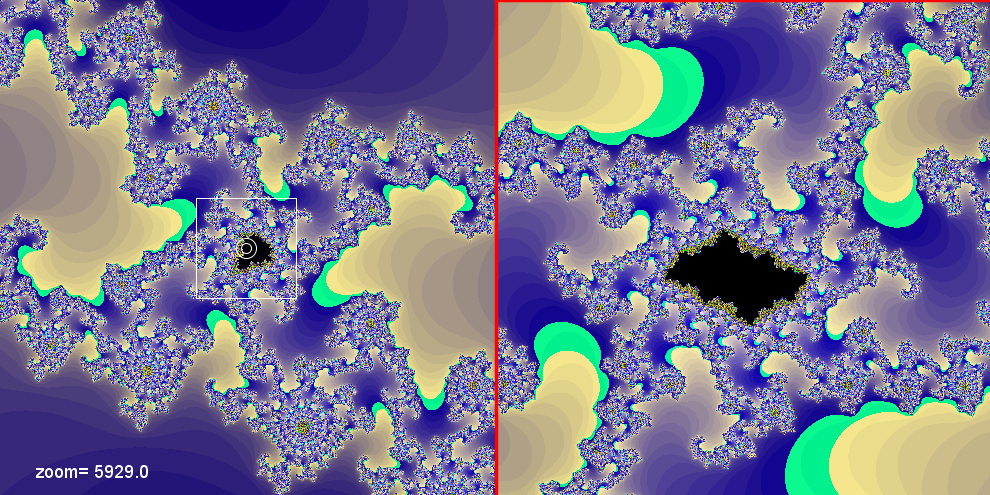
Come potete vedere, le immagini dell'insieme di Julia seguenti, quelle a destra sono molto simile a quella dell'insieme di Mandelbrot a sinistra, nonostante siano due insiemi diversi.

>

>

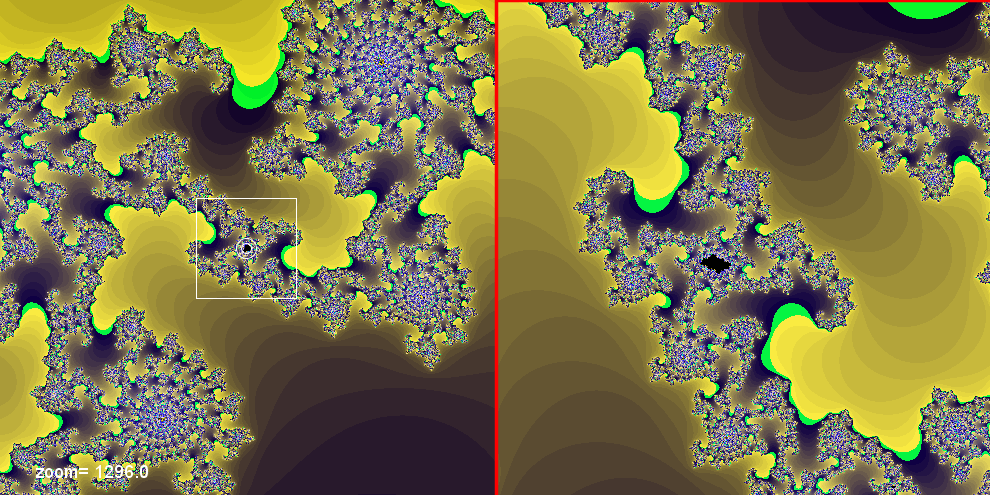
I due insiemi a questi ingrandimenti presentano lo stesso andamento,
l'insieme di Mandelbrot a sinistra quello di Julia a destra hanno al centro una riproduzione del loro insieme.

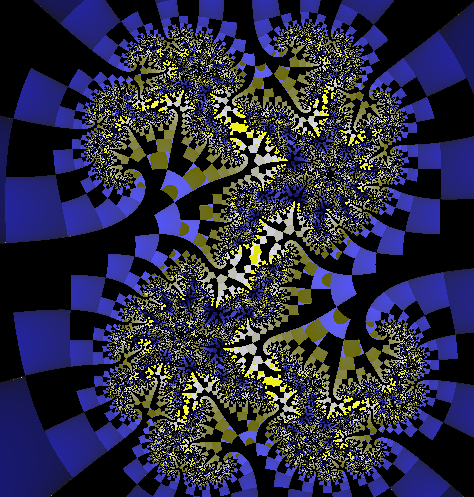
Immagini dell'insieme di Julia

Alcune immagini di Julia a mio parere particolarmente belle

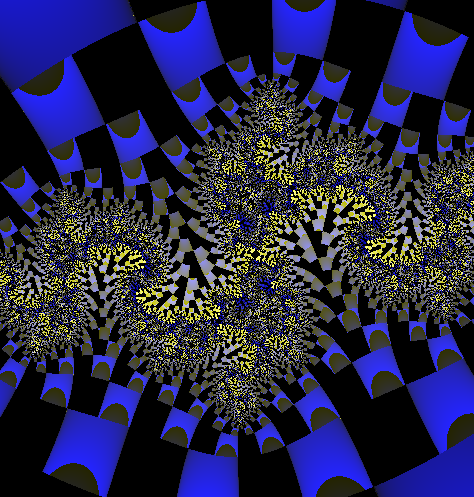
Alcune immagini di Julia che sembrano tridimensional

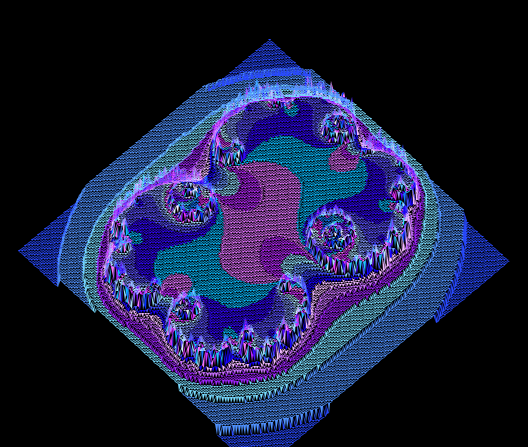
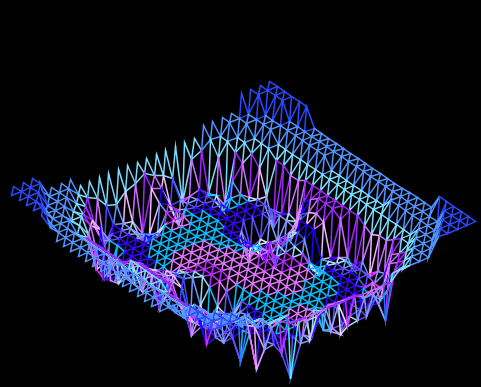
Queste ultime due per apprezzarle necessitano degli occhiali con una lente rossa e una verde

In questo video potete vedere una serie di insieme di julia .
Noterete alla fine del filmato che l'insieme si presenta in tanti pezzettini, sono dette immagini non connesse dell'insieme di Julia, evidentemente ci sono dei punti dell'insieme che si presenta connesso.